Introduction

Une sphère en oxyde de métal est sortie d'un four à 400°C, puis laissée à l'air ambiant (25 °C). Une fois une température de 335°C atteinte, elle est brutalement trempée dans de l'eau à 20°C.

• Données :

• sphère :
  
  
  • rayon = 5 mm
  • k = 20 W/K•m
  • ρ = 3000 kg/m³
  • C = 1000 J/kg•K


• Echanges thermiques :
  
  
  • h_air (°C) = 10 W/K•m²
  • h_eau (°C) = 6000 W/K•m²

Question / Réponse

• Quel est la durée pour atteindre 335°C ? Quel temps faut-il pour que le centre de la sphère atteigne 50°C une fois plongée dans l'eau ? transférée au pipeline ?

• Réponses :

• Exemple : t_335°C = 94 s, t_50°C = 97.1 s ( durée à 50°C : 3.1 s)
  
• Simulation : t_335°C = 97.8 s, t_50°C = 100.6 s ( durée à 50°C : 2.8 s)
  

Valeurs de t tel que T° = 335°C, puis T° = 50°C

• Notes : L'exemple utilise une approche théorique oû la température dans la sphère est supposée uniforme, la simulation est ici plus précise.

Compléments

Pour trouver la solution, on procède en trois étapes :

• Refroidissement à 20 °C (air) pendant 150 s
• Refroidissement à 20 °C (eau) pendant 50 s
• Mesure du temps tel que T_sphere = 335°C

Initialement, la définition du coefficient de convection de la surface de la sphère est :

α = 10×impulse(t,0,150) + 6000×impulse(t,150,200)

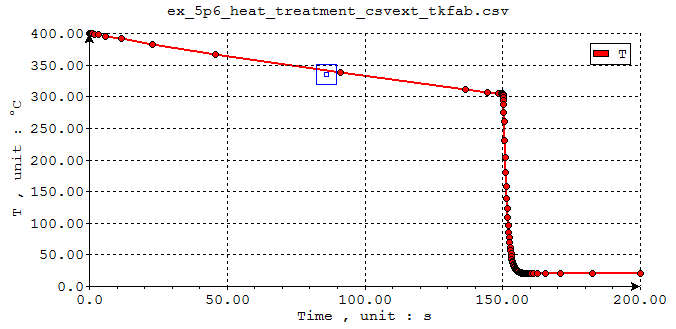
Tracé avec TkFab® de la température en (0,0)

Valeur de t tel que T° = 335°C

Le coefficient de convection de la surface de la sphère devient :

10×impulse(t,0,97.25) + 6000×impulse(t,97.25,200)

Fichiers

• Téléchargement : Fichiers Pro (≅ 350 noeuds)   (400 Ko) - une version "student" est possible avec une symétrie avec l'axe des "y", soit un quart de sphère