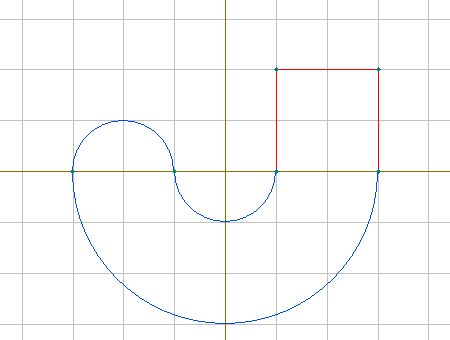Introduction
(
Dimensions initiales sur le site de MSC Software
)
Ce premier design est très simple, voire peu réaliste ( la fixation est excentrée )
mais il permet d'être un exemple facile à réaliser :
Puis :
|
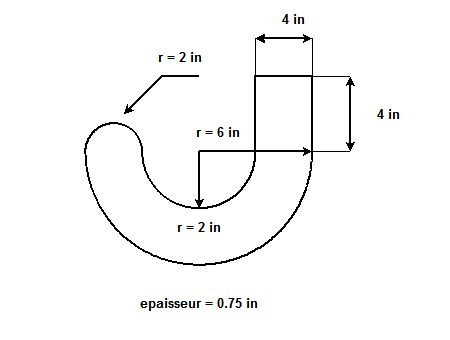
Dimensions.
|
Définition du problème
-
Après la sélection "File / New problem" , une fenêtre apparaît : sélectionnez "Stress Analysis".
-
Unité de longueur en "Inches".
-
Formulation : "plain strain" (le problème étant considéré d'épaisseur suffisante).
-
L'épaisseur du problème (axe Z) est définie par la classe du modèle (Plane-parallel),
ce qui permet de définir une épaisseur de 0.75 in.
|
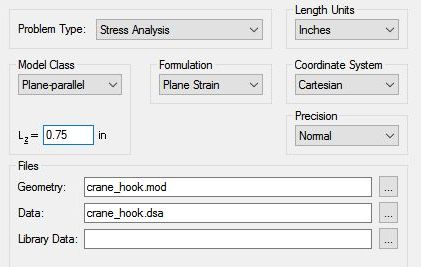
Caractéristiques du problème.
|
Définition de la géométrie (1/2)
-
Après la sélection "Edit Geometry" , une fenêtre apparaît : sélectionnez "Insert Shape" puis le choix "Circle".
-
Tracer un cercle de diametre 4 de centre (0,0).
-
Tracer un cercle de diametre 12 de centre (0,0).
-
Enfin un cercle de diametre 4 de centre (-4,0).
-
Cliquez sur "Zoom to fit".
|
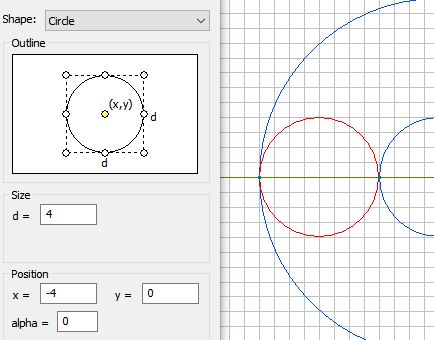
Construction cercles ("clic" = zoom out).
|
Définition de la géométrie (2/2)
-
Cliquez sur "Insert vertices/edges".
-
Supprimez tous les demi-cercles supérieurs.
-
Après un clic droit et "Grid settings", mettre un pas de 1 in.
-
On ajoute les segments comme ci-contre, et on supprime le demi-cercle de gauche.
-
En cliquant à l'intérieur du "J", le bloc entier doit être sélectionné.
|
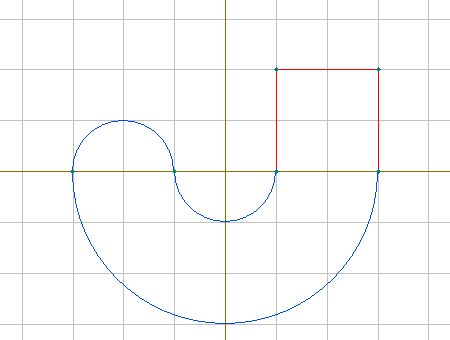
Construction complète.
|
Données
-
On définit un
block
"acier" que l'on associe à la forme principale, on prend E = 200 Gpa et Re = 250 Mpa
-
Un
edge
"ref hor" oû l'on interdit tout déplacement, ce qui correspond plus à un
pire cas qu'à la réalité.
.
-
Un second
edge
"charge" est défini géometriquement comme montré ci-contre. Ainsi qu'un
vertex
de même nom. Ils sont définis par l'interection du demi-cercle avec
trois segments verticaux que l'on supprime ensuite.
-
Le
vertex
"charge" servira à appliquer la charge de 5 000 lb qui est calculée comme suit :
charge en N : 5000•0.453592•9.81 = 22 248 N
soit 22 248 / ( 2.54e-2•0.75 ) = 1 167 900 N/m
(charge linéique sur l'épaisseur)
|
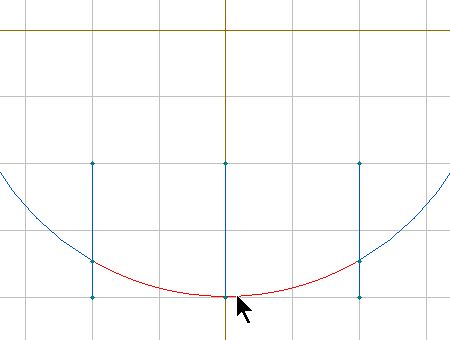
Emplacement de la charge.
|
Simulations
Pour la première simulation, les données du problème doivent
être définies comme ci-contre, c'est-à-dire, la
charge définie sur un segment et ignorée.
Le maillage étant fait automatiquement, on pourra affiner le maillage une seconde fois.
Voir "charge linéique" ci-dessous pour le résultat obtenu.
Pour la seconde simulation, la charge linéique est ignorée; la charge surfacique est donnée par
22 248 / 0.0004889 = 45 506 238 N/m² .
( la surface 0.0004889 est donné par "Integral calculator" du postprocesseur
en utilisant un contour défini par les deux segments "charge").
Voir "charge surfacique" ci-dessous pour le résultat obtenu.
|
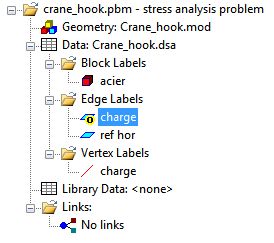
Définition des données.
|
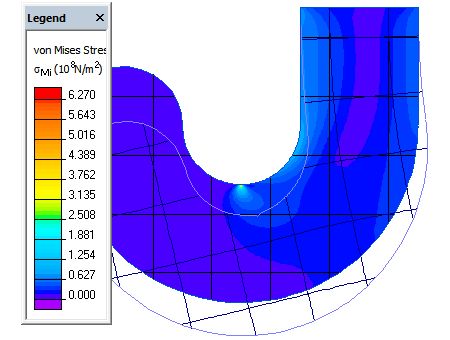
Charge linéique (déformée non à l'échelle).
|
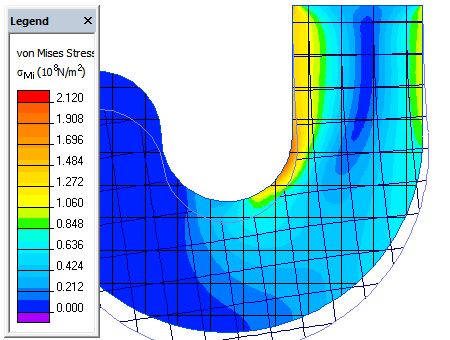
Charge surfacique (déformée non à l'échelle).
|
Fichiers
-
Le design "Student" utilisant la charge linéique n'est pas assez précis.
il nécessite plus de noeuds pour bien déterminer la zone de la charge.
-
En fait c'est un problème de flexion et traction/compression, et on doit utiliser
pour un pré-calcul la notion de moment fléchissant, aboutissant à une
dissymétrie telle que celle ci-dessous :
|
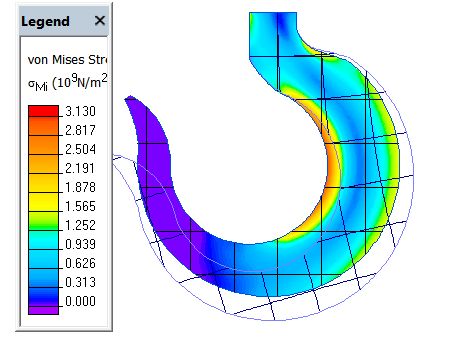
Design optimisé.
|