Introduction
Il y a deux modèles disponibles : thermique et électrique. Puisque l'on s'intéresse
à l'état final d'équilibre, une première solution consiste à
échanger les informations "pertes Joule" et la température respectivement
dans les modèles électrique et thermique jusqu'à convergence.
Une seconde solution consiste à définir quelques zones particulières,
y calculer les pertes Joule et intégrer leurs variations dans le module thermique.
|
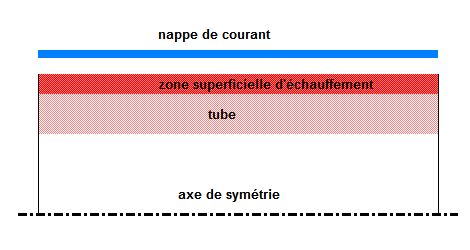
Schéma de principe
|
Première solution : Programmation
C'est la solution proposée par Tera Analysis
(
Modèle original sur le site de QuickField
)
| Parametre |
Valeur |
| Length Units |
Centimeters |
| Lz |
10 cm |
| Model class |
Axisymmetric |
| Frequency |
2500 Hz |
Données communes des problèmes.
Le principe est le suivante :
-
Un programme en Visual Basic résout chaque problème en utilisant
ActiveField™
.
-
Le modèle thermique importe les pertes par effet Joule
calculées par le modèle électrique.
-
Le modèle électrique importe le champ de température
calculé par le modèle thermique.
-
Les deux calculs sont réalisés successivement n fois
(voir courbe ci-contre).
|
-
Programme applicable pour d'autres configurations
-
Import naturel des champs (température, énergie) cest donc une solution
dont le calcul est précis et automatique. Le critère de convergence peut être
modifié si l'on souhaite conserver cette précision.
-
Connaissance d'ActiveField et VBA
-
La conductivité doit être définie par une fonction non-linéaire
de la température dans le modèle électrique.
-
C'est la température moyenne du tube qui sert de critère, cette solution
ne s'applique donc qu'à un bon conducteur de la chaleur et ceci
pour un traitement de surface relativement épais.
-
Nécessite plusieurs pas de calculs
|
Seconde solution : Q = f(T)
Le principe est de définir les pertes Joule par un terme fixe
et un terme dépendant de la température
Ptotal = PT0 + ΔPT
avec
PT0 : pertes Joule importées du modèle électrique calculé à T0
ΔPT : pertes Joule dues à la variation de résistivité.
En effet, si les pertes Joule sont assimilées à la relation :
Ptotal = R•I² = RT0(1 + α(T - T0))•I²
avec α coefficient de température de résistivité.
Soit : Ptotal = PT0 + PT0•α•ΔT
Le processus est donc le suivant : relevé de PT0 puis calcul à
deux température différentes de l'expression PT0•α•ΔT
que l'on indique dans le tableau définissant la puissance volumique de la source thermique,
"Volume Power of the Heat Source".
Pour chacun des
blocks
(ici trois - voir image ci-contre), on relève la valeur Average Value (Joule Heat)
que l'on divise par la valeur Volume, disponible dans Integral Calculator. La division
donne une puissance volumique PT0. Si α = 0,004 alors :
-
0,004•100•PT0 donne un point à 373 K
-
0,004•200•PT0 donne un point à 473 K
|
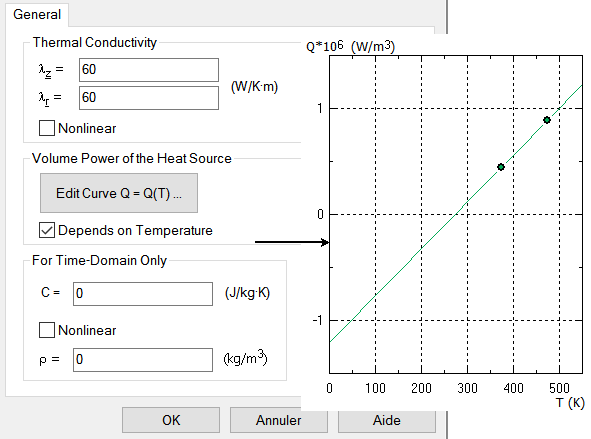
Propriétés thermique d'un bloc "tube".
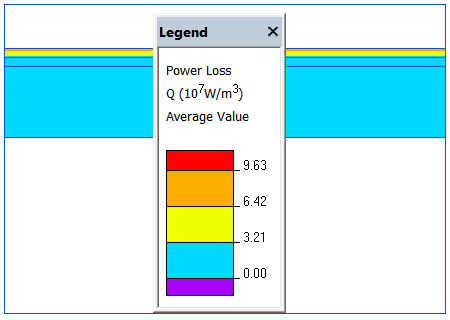
Décomposition en "blocks" : tube 0, tube 1, tube 2
|
-
Pas de programmation.
-
Deux simulations seulement.
-
Modèle lineaire.
-
Appréciation manuelle de la décomposition en
blocks.
-
Quelques calculs intermédiaires.
-
Non adapté à une géométrie complexe.
|
Algorithmes et fichiers des deux solutions
|
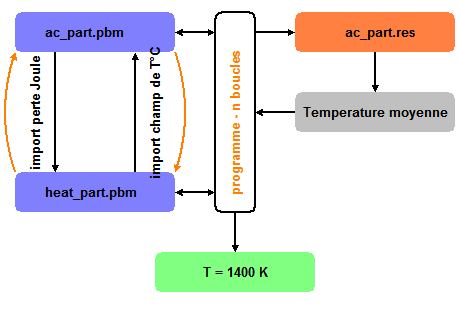
Algorithme de la première solution.
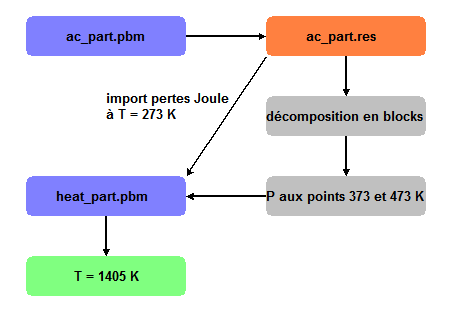
Algorithme de la seconde solution.
|




