Introduction

Le cas où l'échange thermique se fait à température constante est le second cas à bien connaître. dans le cas d'écoulements internes. Pour rappel dans les échanges thermique avec flux interne forcé, il y a deux cas importants :

•   Source infinie
•   Changement de phase

• Exemple avec changement de phase.
• Formulation et données.
• Résultats.
• Fichiers.

Exemple avec changement de phase

L'exemple utilisé est un tube est dans dans un environnement tel que de la vapeur d'eau se condense sur sa surface externe.

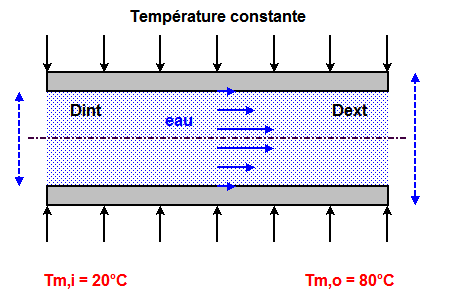
Tube de refroidissement

Formulation et données

• Formulation :

h_m = [(ρ_m • C_p)/ πD_intL] [ ( T_m,o - T_m,i ) / ΔT_lm ] [1]
ΔT_lm est la moyenne logarithmique de la différence de température, définie par :

ΔT_lm = ( ΔT_s - ΔT_e ) / Ln(ΔT_s / ΔT_e )
ΔT_lm = ( (T_s - T_m,o) - (T_s - T_m,i) ) / Ln((T_s - T_m,o) / (T_s - T_m,i)).

[1] Fundamentals of Heat and Mass Transfer, Chapitre - Internal Flow, F.P. Incropera - D. P. De Witt, Editeur Wiley

• Données :

• tube en acier : D_int = 6 cm, D_ext = 8 cm, longueur L = 1m
• liquide : eau, température entrée/sortie :
  T_m,i = 20°C / T_m,o = 80°C
• débit massique de l'eau : ρ_m = 0.25 kg/s
• chaleur specifique de l'eau : C_p = 4181 J/kg.K
• Température du tube : T_s = 100 °C

Résultats

Ici : ΔT_lm = ( 20 - 50 ) / Ln(20 / 50) = 43.3 K et donc h_m = 7681 W/m²K.

D'autre part, si T₀ (Notation Quickfield) = T(x)_m
(température moyenne du liquide à l'abscisse x), nous avons :

T₀ = T_s - (T_s - T_m,i) × e^{-(π • D_int • x • h_m) / (ρ_m • C_p)}. [1]

Ici T₀ = 373-80*pow(0.25,x)

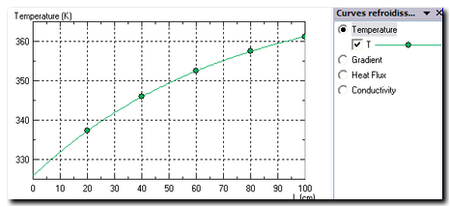
Température le long du diamètre intérieur - D_ext = 8 cm

Fichiers

• Modèle de tube avec refroidissement par température constante   (27 Ko - 1400 noeuds)